
竹とんぼの理論
竹とんぼを安定して飛ばせるには、竹とんぼの理論で、竹とんぼの全体の機構を解析する必要があります。
竹とんぼの機構を解析するための条件は数多くあるので、条件を変更しても、すぐに結果を確認できるシュミレーション機能が必須です。
今回はExcelを使い、このシュミレーションが出来るようにしました。スーパー竹とんぼの純竹タイプを3D-CADを使って描いてみました。実際に設計した寸法ではありませんが、出来るだけイメージが理解できるように描きました。
…… ちょっと一言 ……
竹とんぼを理論的に検討することは、無駄をなくし、効率的に飛行させることが可能です。飛行力学による揚力の検討は次の世代でお願いします。
理論が、高いレベルのスーパー竹トンボの製作を目指す人の参考になれば幸いです。
■更新内容(サイト全体): 更新情報
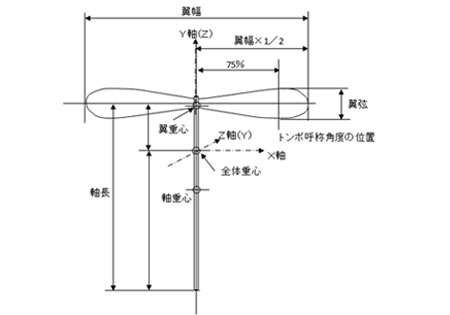
竹とんぼの寸法(写真をクリック)
竹とんぼを理論的に検討するために、基本名称を左図のように決めています。
座標軸のY軸とZ軸は一般的な名称と逆になっています。(これは修正する必要があります)

翼の気流
竹とんぼの理論を論ずる前に、空気の流れが、翼のどの部分でどのような状況かを観察します。
線香を一列に並べ、煙を翼の軸位置から翼端まで均等に流し、煙の変化を見たものです。写真から読み取れることは次の項目です。
(1)煙は軸から翼端までの長さの70~80%前後に収斂されます。(2)85%位から翼端までは気流は見えません。これは翼が押し出した空気が、後ろから前に戻ってしまうためで、目に見えないだけのことと思います。この逆流は誘導抵抗の形で飛行に大きな影響を与えます。

翼の気流
前の写真と同じですが、翼端での気流の乱れが見られます。竹とんぼの形状を変えてもほぼ同じ現象です。これらの現象を考慮して、竹とんぼの形状を設計するための参考にします。
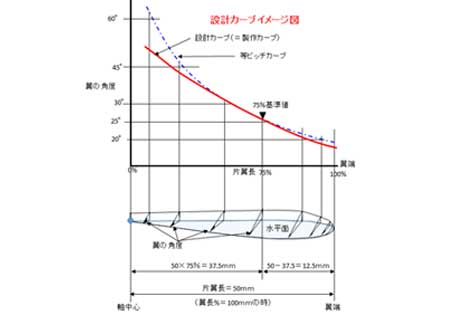
翼の角度(写真をクリック)
軸から翼端まで、急な角度から水平近くになるように角度を変えます。この理由は、軸からの距離にかかわらず、翼が一回転する間に、翼が送り出す空気量を一定にするためです。この角度の変化をピッチ角として表現します。
よってピッチを一定にしたカーブ(角度)で羽根を削れば、翼のどの部分でも同じ空気量を送り出すことができます。グラフは横軸を軸中心から翼端までの距離、縦軸は翼の角度を示します。
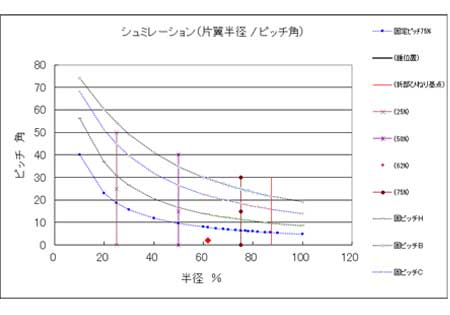
等ピッチカーブ
竹とんぼの翼の角度の呼称を軸から翼端までの長さの75%の位置とします。
左図のグラフに4本のカーブがあります。各カーブを呼ぶ時は、75%の位置の角度で区別します。
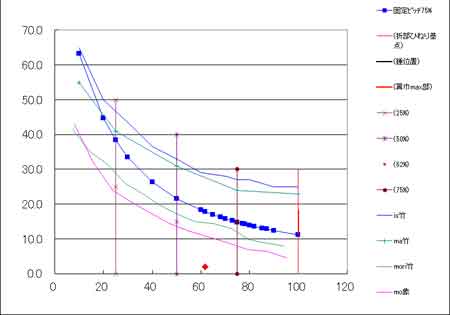
実際の竹とんぼのカーブ
実際の竹とんぼの角度を測ったグラフと等ピッチカーブの例を記入してあります。青い丸の付いた青色線が等ピッチカーブでその他は実機です。実機カーブは大まかな測定のため折れ線となっています。(実機毎に等ピッチカーブは描いていません)
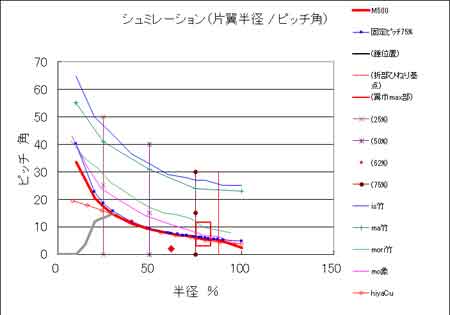
良く飛ぶ竹とんぼとは
説明用に作成したグラフです。
太く赤い線は、シュミレーションして描いたカーブです。赤線とほぼ重なっている細く青い線がありますが、これが等ピッチカーブです。
この赤いカーブは翼の外形寸法、翼の厚さ、軸の長さ、太さ、錘の形状などを変えながら、等ピッチカーブの青いカーブに近づけたものです。
良く飛ぶための条件として、次に示すグラフを考慮する他、各部の重量、翼面積、翼面荷重、慣性モーメント、静止回転数など多くの項目を、決める必要があります。翼端の誘導抵抗の回避と、翼の75%近くの角度を一部変える検討も必要です。
竹とんぼの軸の特性は飛行に大きな影響を与えます。軸の剛性と直線性が大きな要素となります。竹とんぼを飛ばす範囲内で、カーボン材に匹敵する機能を持つ竹軸が必要です。
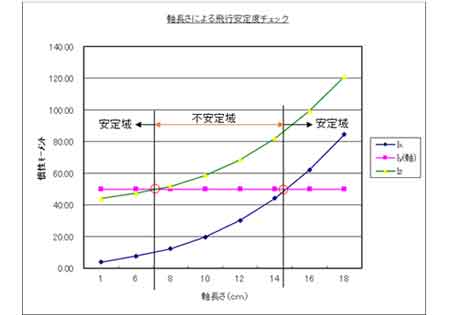
竹とんぼの安定条件(写真をクリック)
竹とんぼが安定に飛ぶための最適値な軸の長さは、グラフ(例)に示されます。(縦軸が慣性モーメント、横軸が竹軸の長さ)。
”テニスラケットの定理”で安定な条件は次の通りです。
(1)回転軸の慣性モーメント(赤色)が最大又は最少の時は安定する。
(2)中間の時は不安定となる。この結果をグラフに表示してあります。
これによれば軸長=7cm以下と14.5cm以上で安定して飛行することがわかります。
すなわち、軸が無いトンボは軸長=0のため安定して飛びます。
グラフは純竹であれ、象嵌であれ、値が違うのみでほぼ同じスタイルです。このグラフは純竹クラスの一例です。実際には横風の影響などの外乱があるため、多少長くします。
***これで昔から抱いていた疑問が解けました。***
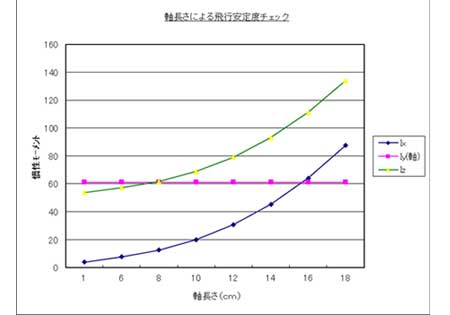
竹とんぼの安定条件
慣性モーメントは竹トンボの軸を回す時の力、とイメージできます。グラフで赤線が直線で示されるのは、トンボ軸のどの部分を回しても同じ力のためです。
このグラフは象嵌トンボの一例です。象嵌は小さい翼でも慣性モーメントを大きく出来るので、赤線が純竹より上にできます。腕力が強い人は慣性モーメントを大きくすることができます。
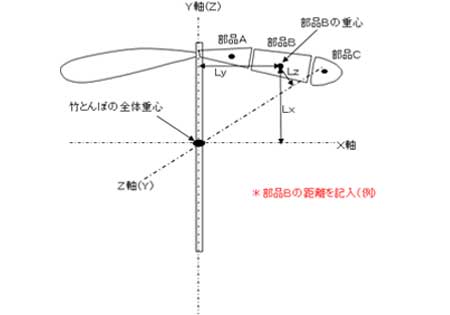
慣性モーメントの計算
慣性モーメントの求めかた:翼をいくつかの部品に分割します。各部品の重心から、竹トンボの全体の重心(軸上にある)を通るX、Y,Zの各軸までの距離を求め、次の式で求めます。
”平行軸の定理”により
慣性モーメント=(部品の重量)×(部品の重心と全体の重心の距離の二乗)+Iay
(注)Iayは形状により決まる部品の慣性モーメント。
この式を部品ごと、軸毎に求め加算してグラフを求める。内容としては中学程度ですが、条件が多いので手計算ではたいへんです。
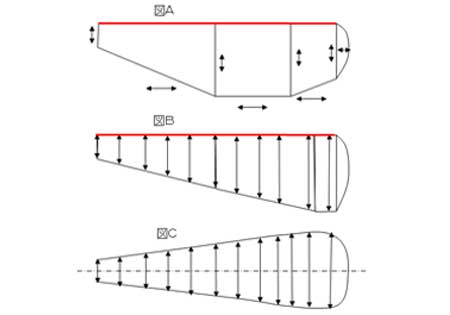
実際の翼の設計例
図AはPCで計算するための基本の翼図です。赤線はPCで計算しやすいように直線にしてあります。矢印の寸法は自由に設定できます。図Bは実際に計算した平面図の例です。図Bの多数の矢印は、長さと角度を持ったベクトルです。
図Cはベクトル位置を動かして新たにデザインしたものです。
図Cは翼の重心の位置が変わるため、慣性モーメントが変化しますが、誤差を無視しています。
尚、図Bで製作しても支障はありませんが、図Cは自由度を持たせるため、参考に作りました。
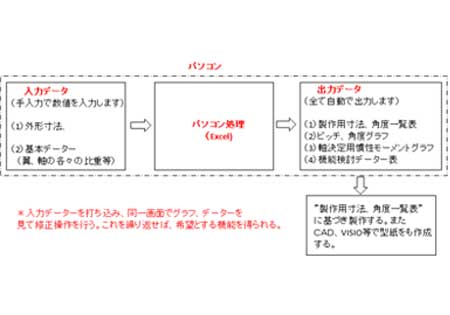
PCの内部構成(写真をクリック)
平面だけでなく、厚さ方向も計算に含まれます。軸から翼端までの翼の角度を細かく表示します。尚面積は投影平面でなく、実平面示します。
主な入力値は外形寸法の他、比重(錘、翼、軸)、軸の長さ、翼端低減角、その他です。
外形寸法が決定したら、手動ですが、図形作成ソフトで作図し、出力図をそのまま型紙にします。

出力表の一部(写真をクリック)
表はシュミレーションで出力する項目です。実際に削るための、角度や寸法類は別に出力されます。(数値は例です)
翼や軸のデーターを変えると、即座に表の数値は変わります。その数値が最適値と思われるまで,入力値を変え設計します。

スーパー竹とんぼ3D-CAD 姿図1(写真をクリック)
3D CADを使って作図してみた。CADは初めてのため、四苦八苦し、出来具合は100点にはほど遠いが、何とか仕上がった。翼の角ばった箇所はもっとデーターを増やせば滑らかにできる。
ソフトはフリー版を使用した。機能はそこそこらしいが、昔なら100万円以上するものが、無償で使えるのはありがたい。この種ものは海外製がほとんどで、この分野では日本はかなり遅れていて?、後進国?のような気がする。翼の型紙も別の海外製のフリーソフトで作図している。
同じソフトの有償版を使えば、3Dプリンターを使ってこの実像の印刷が可能(全翼長13cm)。
実際に設計した形状ではないが、削る箇所の要点は同じ。軸の説明は将来記述するが、竹に熱を加え、ネジリ、圧力を強制的に加え、ネジリ強度と直線性をUPさせている。(図2でも軸のねじりを表現してみた)
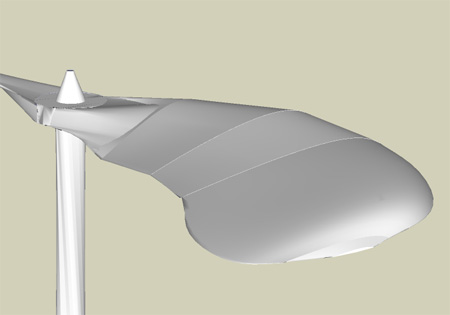
スーパー竹とんぼ3D-CAD 姿図2(写真をクリック)
翼の下流側エッジ(図の左下側)は薄く鋭く削り、翼の巾を飛行機の翼のように少し流線型に湾曲させる。どのような飛行特性にするかで厚さや翼幅、角度等が決まる。実際の形状はシュミレーションソフトで作成し、寸法を決めている。翼を削るのは単純ではなく、削り方のノウハウもあり複雑である。

スーパー竹とんぼ3D-CAD 姿図3(写真をクリック)
正面から見た翼。左側の翼端は重くし、錘にするため薄く削っていない。軸近くから錘付近までは重量を少なくするため、できるだけ肉厚を薄くする。翼は少しひねった?つもり。

スーパー竹とんぼ3D-CAD 姿図4(写真をクリック)
側面から見た図。この作例は翼端の角度を低減させていない。実際に削るテクニックやノウハウは経験豊富な人に教えを乞うしかない。